Working with reduced datasets by exploiting sparsity
Insights from compressed sensing (intro 2006) for real-world AI
Think:
1. Satellites doing hyper/multi-spectral imaging and communications
2. Drones and UAVs doing surveillance, wildfire monitoring, and imaging
3. Smart sensors ensuring upkeep of industrial machines
4. Underwater unmanned vehicles collecting and transmitting data under severe resource constraints
Applications across space, air, land, and sea are generating TeraBytes of multi-modal sensor data. Should we just throw more resources to make sense from all this data or is there a smarter way?
A foundational insight is that: Real world data collected from sensors like vibration, acoustics, images, videos, spectroscopy, etc. is very sparse. When transformed into the Fourier domain for instance, the raw data can be efficiently represented by very few parameters. Reduction to and below 1% of the raw data is achievable for several data types.
By leveraging this insight, Candes et al. in 2006 developed a novel technique called compressed sensing, which exploits sparsity of real world data to collect a small fraction of raw data in comparison to that required by the Shannon-Nyquist sampling theorem.
This is food for thought as we develop novel machine learning techniques to analyze terabytes of sensor data being generated from a variety of applications spanning from satellites to unmanned underwater vehicles. You can read our recent paper in Procedia CIRP addressing this problem here.
Let’s look at an example:
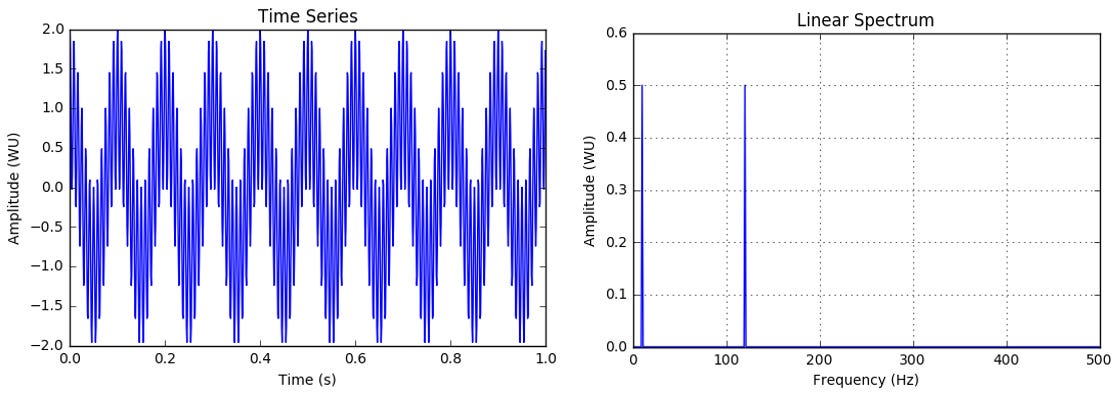
The following figure shows a simulated vibration signal sampled at 1000 Hz having 2 frequencies - 10 Hz and 120 Hz, and its linear spectrum (Fourier Transform).
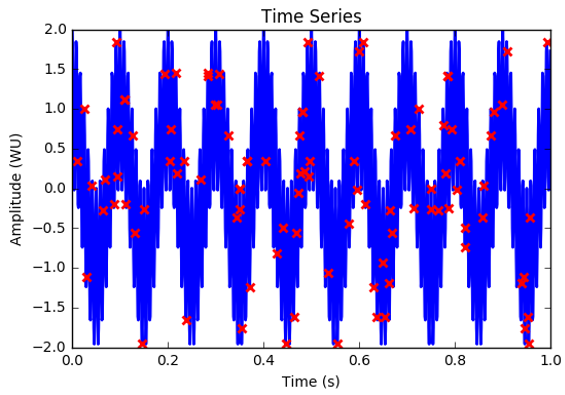
Now, we will collect only a small fraction of the raw data, 10% in this case. 100 datapoints instead of 1000 datapoints.
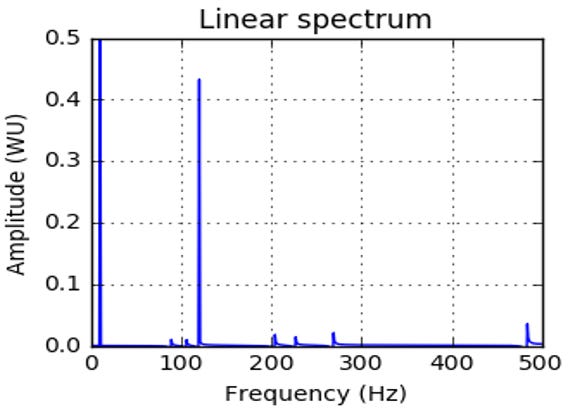
Next, we apply compressed sensing to recover the full signal using just 10% undersampled measurements. The following figure shows the reconstructed peaks at 10 and 120 Hz.
Now, let’s look at an actual vibration calibration signal:
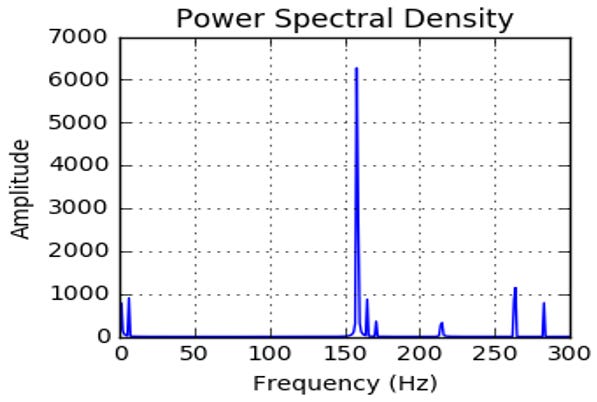
The following figure shows an actual vibration signal sampled at 600 Hz having a calibration frequency of 159 Hz (with a certain SNR), and its linear spectrum (Fourier Transform).
Now, we will again collect only a small fraction of the raw data, 10% in this case. 120 datapoints instead of 1200 datapoints.
Next, we apply compressed sensing to recover the full signal using just 10% undersampled measurements. The following figure shows the reconstructed peak at 159 Hz with a certain SNR.
As seen in the above two examples, we can reconstruct original signals using just 10% of the raw data using compressed sensing. A few good papers to read are this, this, and this. As mentioned previously, this technique exploits the sparse structure in real-world data to enable collecting a small fraction of the raw data while ensuring reconstruction guarantees.
For the machine learning folks, the insight here is that good latent representations learnt from undersampled measurements can preserve signal information. An interesting question is how to develop novel architectures that leverage this insight to solve different downstream problems using a small fraction (~10%) of the raw data.
This will enable >10x efficiency gains in the training of machine learning models for real world AI application.
You can read more about our mission of ‘Learning to predict using just the 10% important data’ at Lightscline, here.